UNIFIED GROWTH THEORY
Research and Articles
The evolution of economies during the major portion of human history was marked by Malthusian Stagnation. Technological progress and population growth were miniscule by modern standards and the average growth rate of income per capita in various regions of the world was even slower due to the offsetting effect of population growth on the expansion of resources per capita. In the past two centuries, in contrast, the pace of technological progress increased significantly in association with the process of industrialization. Various regions of the world departed from the Malthusian trap and experienced initially a considerable rise in the growth rates of income per capita and population. Unlike episodes of technological progress in the pre-Industrial Revolution era that failed to generate sustained economic growth, the increasing role of human capital in the production process in the second phase of industrialization ultimately prompted a demographic transition, liberating the gains in productivity from the counterbalancing effects of population growth. The decline in the growth rate of population, and the associated enhancement of technological progress and human capital formation, paved the way for the emergence of the modern state of sustained economic growth.
The transition from stagnation to growth and the associated phenomenon of the great divergence have been the subject of intensive research in the growth literature in recent years. The discrepancy between the predictions of exogenous and endogenous growth models, and the process of development over most of human history, induced growth theorists to advance an alternative theory that would capture in a single unified framework the contemporary era of sustained economic growth, the epoch of Malthusian stagnation that had characterized most of the process of development, and the fundamental driving forces of the recent transition between these distinct regimes.
The preoccupation of growth theory with empirical regularities that have characterized the growth process of developed economies in the past century and of less developed economies in the last few decades, has become harder to justify from a scientific viewpoint in light of the existence of vast evidence about qualitatively different empirical regularities that characterized the growth process over most of human existence. It has become evident that in the absence of a unified growth theory that is consistent with the entire process of development, the understanding of the contemporary growth process would be incomplete and distorted. As stated eloquently by Copernicus: "It is as though an artist were to gather the hands, feet, head and other members for his images from diverse models, each part perfectly drawn, but not related to a single body, and since they in no way match each other, the result would be monster rather than man."
The evolution of theories in older scientific disciplines suggests that theories that are founded on the basis of a subset of the existing observations and their driving forces may be attractive in the short run, but non-robust and eventually non-durable in the long run. The attempts to develop unified theories in physics have been based on the conviction that all physical phenomena should be explainable by some underlying unity. Similarly, the entire process of development and its fundamental forces ought to be captured by a unified growth theory.
The advancement of unified growth theory was fueled by the conviction that the understanding of the contemporary growth process would be limited unless growth theory was based on micro-foundations that would reflect the qualitative aspects of the growth process in its entirety. In particular, the hurdles faced by less developed economies in reaching a state of sustained economic growth would remain obscured unless the origin of the transition of the currently developed economies into a state of sustained economic growth would be identified, and its implications would be modified to account for the additional economic forces faced by less developed economies in an interdependent world.
Unified growth theory suggests that the transition from stagnation to growth is an inevitable outcome of the process of development. The inherent Malthusian interaction between the level of technology and the size and the composition of the population accelerated the pace of technological progress, and ultimately raised the importance of human capital in the production process. The rise in the demand for human capital in the second phase of industrialization, and its impact on the formation of human capital, as well as on the onset of the demographic transition, brought about significant technological advancements, along with a reduction in fertility rates and population growth, enabling economies to convert a larger share of the fruits of factor accumulation and technological progress into growth of income per capita, and paving the way for the emergence of sustained economic growth. Moreover, the theory suggests that differences in the timing of the take-off from stagnation to growth across countries contributed significantly to the Great Divergence and to the emergence of convergence clubs.
Variations in the timing of the transition from stagnation to growth, and thus in economic performance across countries (e.g., England's earlier industrialization in comparison to China), reflect initial differences in geographical factors and historical accidents and their manifestation in variations in institutional, demographic, and cultural factors, trade patterns, colonial status, and public policy. In particular, once a technologically-driven demand for human capital emerged in the second phase of industrialization, the prevalence of human capital promoting institutions determined the extensiveness of human capital formation, the timing of the demographic transition, and the pace of the transition from stagnation to growth. Thus, unified growth theory provides the natural framework of analysis in which variations in the economic performance across countries and regions could be examined based on the effect of variations in educational, institutional, geographical, and cultural factors on the pace of the transition from stagnation to growth.
The establishment of a unified growth theory has been a great intellectual challenge, requiring major methodological innovations in the construction of dynamical systems that could capture the complexity which characterized the evolution of economies from a Malthusian epoch to a state of sustained economic growth. Historical evidence suggests that the transition from the Malthusian epoch to a state of sustained economic growth, rapid as it may appear, was a gradual process and thus could not plausibly be viewed as the outcome of a major exogenous shock that shifted economies from the basin of attraction of the Malthusian epoch into the basin of attraction of the Modern Growth Regime. The simplest methodology for the generation of this phase transition -- a major shock in an environment characterized by multiple locally stable equilibria -- was, therefore, not applicable for the generation of the observed transition from stagnation to growth.
An alternative methodology for the observed phase transition was rather difficult to establish since a unified growth theory in which economies take-off gradually but swiftly from an epoch of a stable Malthusian stagnation would necessitate a gradual escape from an absorbing (stable) equilibrium -- a contradiction to the essence of a stable equilibrium. Ultimately, however, it has become apparent that the observed rapid, continuous, phase transition would be captured by a single dynamical system, if the set of steady-state equilibria and their stability would be altered qualitatively in the process of development. As proposed in unified growth theory during the Malthusian epoch the dynamical system would have to be characterized by a stable Malthusian equilibrium, but ultimately, due to the evolution of latent state variables, the dynamical system would change qualitatively, the Malthusian equilibrium would vanish endogenously, leaving the arena to the gravitational forces of the emerging Modern Growth Regime, and permitting the economy to take-off and to converge to a modern growth steady-state equilibrium.
UNIFIED GROWTH THEORY

Galor, O. (2011). Unified growth theory. Princeton University Press.
Unified Growth Theory provides a fundamental framework of analysis for the evolution of individuals, societies, and economies over the entire course of human history. The theory captures in a single analytical framework the main characteristics of the process of development: (i) the epoch of Malthusian stagnation that has characterized most of human history; (ii) the escape from the Malthusian trap and the associated spike in the growth rates of income per capita and population; (iii) the emergence of human capital formation in the process of development; (iv) the onset of the demographic transition; (v) the contemporary era of sustained economic growth; and (vi) the divergence in income per capita across countries.
Media Coverage:
TRANSITION ENGINE:
INTERACTION OF
POPULATION SIZE & TECHNOLOGY

Galor, O., & Weil, D. N. (2000). Population, Technology, and Growth: From Malthusian Stagnation to the Demographic Transition and Beyond. American economic review, 90(4), 806-828.
This paper develops a unified growth model that captures the historical evolution of population, technology, and output. It encompasses the endogenous transition between three regimes that have characterized economic development. The economy evolves from a Malthusian regime, where technological progress is slow and population growth prevents any sustained rise in income per capita, into a Post-Malthusian regime, where technological progress rises and population growth absorbs only part of output growth. Ultimately, a demographic transition reverses the positive relationship between income and population growth, and the economy enters a Modern Growth regime, with reduced population growth and sustained income growth.
TRANSITION ENGINE:
INTERACTION OF
ADAPTATION & DEVELOPMENT

Galor, O., & Moav, O. (2002). Natural Selection and the Origin of Economic Growth. Quarterly Journal of Economics, 117(4), 1133-1191.
This research develops an evolutionary growth theory that captures the interplay between the evolution of mankind and economic growth since the emergence of the human species. The theory suggests that the struggle for survival that had characterized most of human existence generated an evolutionary advantage to human traits that were complementary to the growth process, triggering the takeoff from an epoch of stagnation to sustained economic growth.
Media Coverage:
GLOBALIZATION &
TRANSITION PACE OF DC AND LDC
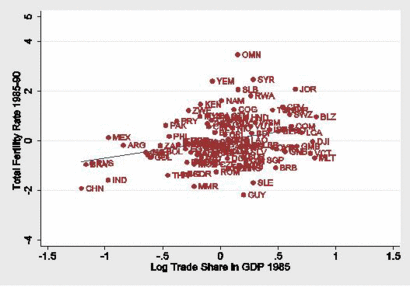
Galor, O., & Mountford, A. (2008). Trading Population for Productivity: Theory and Evidence. Review of Economic Studies, 75(4), 1143-1179.
This research argues that the differential effect of international trade on the demand for human capital across countries has been a major determinant of the distribution of income and population across the globe. In developed countries the gains from trade have been directed towards investment in education and growth in income per capita, whereas a significant portion of these gains in less developed economies has been chanelled towards population growth. Cross-country regressions establish that indeed trade has positive effects on fertility and negative effects on education in non-OECD economies, while inducing fertility decline and human capital formation in OECD economies.
Media Coverage:
TOWARDS A UNIFIED THEORY OF ECONOMIC GROWTH

Snowdon, B. (2008). Towards a unified theory of economic growth: Oded Galor on the Transition from Malthusian Stagnation to Modern Economic growth. World Economics., 9(2), 97-151.
An interview of Oded Galor by Brian Snowdon about the underlying philisophy behind the development of Unified Growth Theory.
THE MALTHUSIAN HYPOTHESIS

Ashraf, Q., & Galor, O. (2011). Dynamics and Stagnation in the Malthusian Epoch. American Economic Review, 101(5), 2003-41.
his paper examines the central hypothesis of the influential Malthusian theory, according to which improvements in the technological environment during the preindustrial era had generated only temporary gains in income per capita, eventually leading to a larger, but not significantly richer, population. Exploiting exogenous sources of cross-country variations in land productivity and the level of technological advancement, the analysis demonstrates that, in accordance with the theory, technological superiority and higher land productivity had significant positive effects on population density but insignificant effects on the standard of living, during the time period 1-1500 CE.
Media Coverage:
